This article was written by Michael Housh, owner of Housh Home Energy and a regular contributor to HVAC School. Thanks, Michael!

This is another article in trying to relate the air side of HVAC with the water side. In this article, I’m going to talk about how to determine pump flow (GPM) based on the pressure difference across the pump.

I relate checking pump flow to checking airflow with static pressure on the air side. Without knowing how many gallons per minute we’re moving, the less we can truly tell about what our system is doing. Most of the equations that revolve around hydronic systems (or air-conditioning systems) revolve around how many pounds of a substance we’re moving through the system.

The trouble with many of the systems out there is that most installers/designers don’t add any way for us to check this in the field. I’ve primarily seen any sort of pressure port or gauge on larger commercial/industrial systems or sometimes on older pump flanges with a pressure port built-in. Today, most people are installing isolation flanges on their pumps, so I strongly encourage everyone to spend a few extra dollars on isolation flanges with a drain port built-in. These can allow a technician or installer a means of checking the pressure difference across the pump.

Measuring pump flow (just like airflow) requires looking at the manufacturer’s charts on the pump you are working on. But instead of checking static pressure across an appliance, we use the pressure difference across the pump. In the U.S., the amount of energy produced by a pump is measured in ft. of head. However, all of the gauges that are used measure in PSI. Luckily, there is a formula to convert PSI -> Ft. of head.

H = PSI / (0.433 * SG)

Where:

H = feet of head

PSI = pounds per square inch

0.433 = constant

SG = specific gravity (for the rule of thumb, we can use 1.02 for water)

The constant (divisor) can be simplified by multiplying 0.433 * 1.02 = 0.44:

H = PSI / 0.44

At this point, I must give a WARNING about some of the pictures I’m going to show, as they will surely be controversial, but until my mind is changed on this subject, Testo will have to remove H₂O from their measurable media type.

Before I move on, let me lay some groundwork. My latest system had a design load of @ 80K BTU. This system utilized two zones, each having a pump. Using the “rule of thumb” sensible heat rate equation for hydronics, I can lay out what my total system GPM should be to deliver the load. Most hydronic systems are designed around a 20° delta T on the distribution side, which is what I’ll use in the below equation (for more on the sensible heat rate equations, you can read this tech-tip I wrote).

80,000 / (500 * 20) = 8 GPM

So, this means that my total system needs to move 8 gallons per minute in order to meet demand. In my scenario, I actually have two zone pumps (one does a bonus room, which needs about 2-3 GPM, and the other does the main house, which needs about 5 GPM). I utilized the same three-speed pump on both zones, and I will cover how I set the speed based on the above GPM that I need to deliver. Below is the pump curve (similar to a fan chart) that we need to compare to, each line representing one of the speeds of the pump.

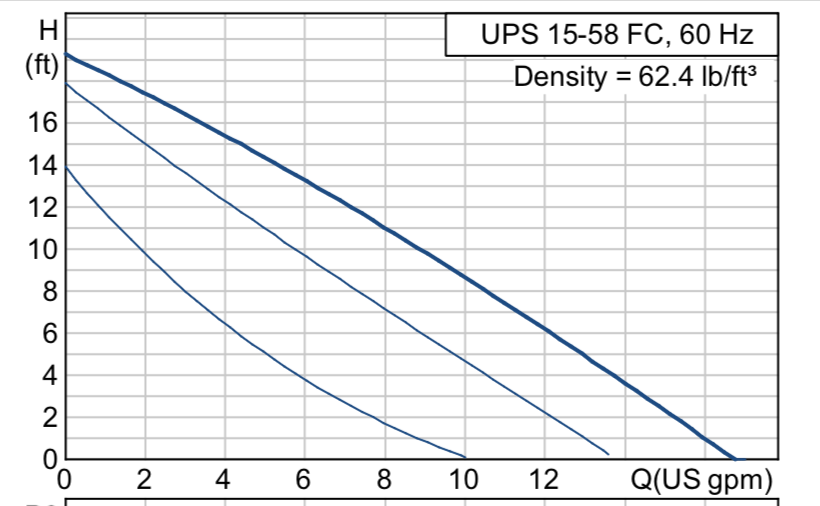
I take the pressure at the inlet and the outlet of the pump to get my delta P, using the drain port on the isolation flanges.    

Delta P = 3.5 PSI (as you can see, this is very hard to take from an analog-style gauge).  I can then convert my delta P to ft. of head using the formula above.

3.5 / 0.44 = 7.95 ft. of Head

We can then compare to the above pump curve (for low speed, lowest curve), which shows a flow rate of about 2.8-3 GPM. That is where I want to be for that zone. I can then do the same for the other zone pump (set on medium speed).

This process gives me a delta P of 4.8 PSI, and we can convert that to get a ft. of head value of 10.9. When comparing my delta P to the medium speed pump curve, my flow rate is about 5 GPM, giving me a total system flow rate of my desired 8 GPM.

To take it a step further, I then compare my system loop delta T, which in this case actually worked out perfectly to 20°. So, I won’t go through the formula again, but this proves that we’re delivering the desired 80K BTU to the space.

—Michael