The general law of perfect gas is a combination of Boyle’s and Charles’s laws. Each of those laws neglected pressure, temperature, or volume in their formulas. The law of perfect gas combines the two, clearly establishing the relationship between all three variables and giving those laws a much more practical use in our field.

We can represent the law of perfect gas with the following equation:

As you can see, you multiply the initial pressure and volume and divide that product by the initial temperature to yield a ratio. That ratio will equal the product of the final pressure and volume divided by the final temperature.

You can solve for any one of these unknown variables if you have all five of the other variables. 

Where might we see the law of perfect gas in HVAC/R?

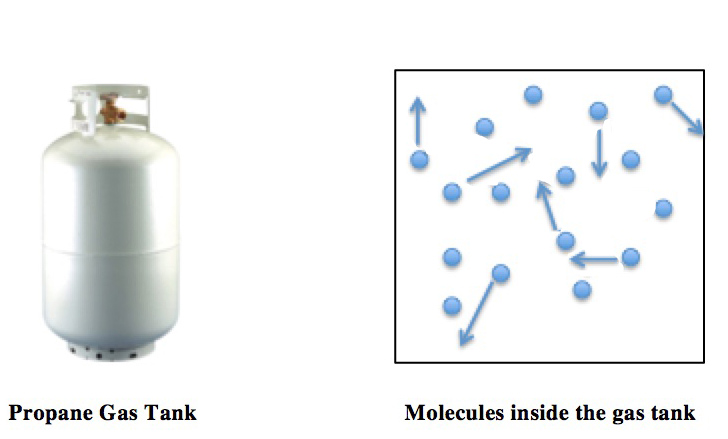
Pressure, temperature, and volume are critical variables to keep track of when storing gas in tanks. As such, you may use the law of perfect gas to monitor changes in the tank’s contents based on environmental conditions.

For example, if the storage area temperature increases, it won’t be long before the tank’s contents get warmer. Heat causes the gas to expand, and the molecules will zoom about more quickly in the same small space, leading to higher pressure. Tanks are rated to withstand specific pressures, but it’s up to us to make sure that we fill and store tanks appropriately to prevent explosions.

BlyumJ, CC BY-SA 4.0, via Wikimedia Commons

As you can see, there is a domino effect between these three variables. When one of them changes, the other two will also undergo predictable changes. However, some conditions will cause gases to break the rules. For example, gases that occupy a closed space cannot chemically react with other gases lest they disrupt the established relationship. Gases will also deviate from the rules when they enter contact with their liquid forms or enter the supercritical state.

What is the gas constant, and how does it relate?

The law of perfect gas has a rearrangeable equation that can yield different values. One of those values is the gas constant.

The law of perfect gas merely establishes the relationship between pressure, temperature, and volume. They are all proportional, and they act on gases at a constant rate. This constant rate varies across chemical elements, but it’s generally called the “gas constant.” You can yield the gas constant by dividing the product of pressure and volume by the temperature.

We use the gas constant in another extension of the perfect gas law: the ideal gas law.

What is the ideal gas law, and how does it relate?

The ideal gas law takes the law of perfect gas a little bit further. Instead of just factoring in the volume, pressure, and temperature, the ideal gas law also accounts for the number of molecules. It does that by including Avogadro’s law. Avogadro’s law states that the volume of a gas (V) is directly proportional to the number of molecules it contains (n). When one increases, the other must also increase proportionally. You can use the following equation to represent Avogadro’s law:

The ideal gas law combines the law of perfect gas, Avogadro’s law, and the gas constant (R) to yield the following equation:

PV = nRT

The ideal gas law establishes a relationship between pressure, volume, temperature, and molecular content that predicts real gases’ behavior. There is no such thing as an ideal gas. Ideal gases do not interact with each other and take up no volume. Those qualities are impossible to achieve by natural standards. As a result, the values you might yield from the ideal gas law equation will deviate a bit from the actual values you might measure.

However, some gases are very close to ideal, so the ideal gas law works well enough to predict approximate gas behaviors when you have the values for all the equation variables.

Let’s say you have every single value except the moles. You can plug the measured volume, moles, universal gas constant (which varies), and temperature to find the approximate pressure. You would merely divide the equation by the gas constant and temperature on both sides to isolate the variable for moles (n). Divide the product of pressure and volume by the product of the gas constant and temperature, and the quotient will be the number of moles. 

References

https://www.hvacrschool.com/gas-law-conceps-for-hvac-r/ 

https://www.hvacrschool.com/how-much-pressure-is-that-recovery-tank-designed-for/

https://www.hvacrschool.com/idea-gas-rulebreakers/

https://www.khanacademy.org/science/physics/thermodynamics/temp-kinetic-theory-ideal-gas-law/a/what-is-the-ideal-gas-law 

Special thanks

Modern Refrigeration and Air Conditioning, 21st edition (Andrew Althouse, Carl Turnquist, Alfred Bracciano, Daniel Bracciano, and Gloria Bracciano)

Refrigeration & Air Conditioning Technology, 9th edition (Eugene Silberstein, Jason Obrzut, John Tomczyk, Bill Whitman, and Bill Johnson)

These truly are the reference guides for the industry and deserve attribution for all such articles.