Get Tech Tips
Subscribe to free tech tips.
Density of Air & Water Part 2
Here is part 2 from Michael Housh from Housh Home Energy in Ohio. Thanks, Michael!
This is part two in a series on a deeper look into the sensible heat rate equations. You can find the first article here HERE if you missed it. This article will dive deeper into the density of “standard air” and water based on a change in temperature. “Standard air” is air with 0% RH and at sea level (14.7 PSIA).
As mentioned in the previous article, density can be defined as its mass per unit of volume (or weight per unit of volume). Another thing I previously mentioned is that the sensible heat rate equations stem from a lower-level equation that is about moving a mass of a fluid.
Let’s look at the equation to find the density of air first. The following equation can be used to determine the density of air for a given pressure and temperature. For all of our equations and graphs, we will use the absolute pressure of 14.7 (the pressure at sea level).
 Formula:
Formula:
We must first convert our temperature to an absolute temperature (Rankine).
Where:
T = Temperature (°F)
Next, we can solve for the density for the given temperature and atmospheric pressure.
![]()
Where:
D = density of air (lb/ft3)
Pa = absolute pressure of air (psia) = 14.7
Tr = temperature (°R) converted in the previous step
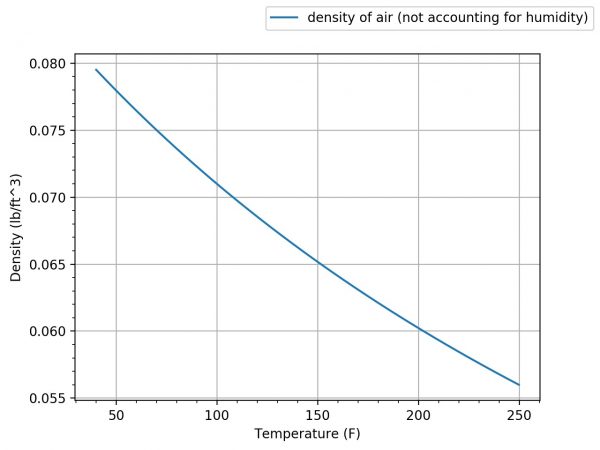
As you can see, we are dealing with pretty minute changes in the density of air based on temperature change when the humidity is 0%.
You can also use the above formula to solve for the density of air at different altitudes. You can do that by substituting Pa with the absolute pressure at a given altitude, but that will be left for you to figure out.
Next, let’s look at the density of water equation. This one is a little more complex. It is also only valid for water temperatures between 50°F and 250°F.
![]()
Where:
D = density of water (lb/ft3)
T = temperature (°F)

As you can see, the density of water has a little more of a drastic change based on temperature than that of air.
First off, when we relate these to the sensible heat rate equations (that are about moving pounds of a fluid), we can see that the mass can be affected by a significant amount (at least in the case of water). Secondly, 1 cubic foot of water weighs significantly more than 1 cubic foot of air.
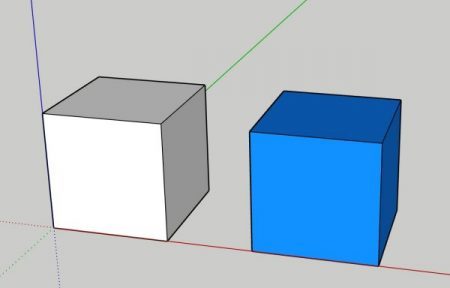
Let’s envision two 1’ x 1’ x 1’ cubes. One is full of air, and the other is full of water. Both of these are at 50°F. Let’s imagine that we have a fan or pump moving one of these cubes each minute. Next, let’s look at how we would compare the BTUs carried/rejected from both of these cubes with 20° delta T.
We are going to use the lower-level equation found in the first article to make this a little easier to understand.
Q = M * C * T
Where:
Q = BTU's absorbed or rejected from the fluid (BTU/hr)
M = mass / density of the fluid (lb/ft3)
C = specific heat (BTU/lb) : Air = .24 & water = 1.0
T = temperature change dry bulb (°F)
When we calculate the density of a fluid that has a temperature change to it, we want to use the density for the average temperature. So, for our experiment, since we are starting at 50° and we end at 70°, we will use the density for water and for air at 60°.

At these parameters, we’d have to move 3,419 more cubic feet of air to achieve the same as 1 cubic foot of water.
So, let’s see how we can use this information to build a little bit of a better equation than the default “standard air” and “standard water” sensible heat rate equations.
Since the density of air is pretty tricky and is affected by both altitude and humidity, I would recommend using the online calculator at HVACR School (third calculator in the left column). With water, I would use the above equation to solve for density or graph above. Remember, we want to use the average temperature to solve for the density for both of these.
Now, let’s rewrite the sensible heat rate equations into a slightly more accurate way to calculate the BTU/h of both air and water:

Let’s run through a little comparison of these equations from the “standard air” and “standard water” equations. I’ll start with the air-side first. Let’s imagine we have a 70° return air temperature and a 130° supply air temperature (a 60° delta T). The relative humidity is 40%, and I used the elevation of my home, which is approximately 800 ft. above sea level. By using the online calculator, I figured the density of the average temperature of the air at these parameters is 0.06857. Now, let’s assume we have 800 CFM moving across our appliance. We can now solve for the BTU transfer of our appliance into the air.
| Standard Air | Improved Air |
| Q=1.08 x 800 x 60 = 51,840 btu/hr | Q = .06857 x 14.4 x 800 x 60 = 47,395 btu/hr |
That is about a 10% difference by correcting for the density of the air.
Next, for the water-side, let’s assume that we have an incoming water temperature of 170° and an outlet water temperature of 190° across a boiler (a 20° delta T). Our pump is moving 5 gallons per minute. The density of water at the average temperature of 180° is 60.59814, so we can now solve for the BTU transfer from the boiler into the water.
| Standard Water | Improved Water |
| Q = 500 x 5 x 20 = 50,000 btu/hr | Q = (60.59814 / 7.48) x 60 x 5 x 20 = 48,605 btu/hr |
That is about a 5% difference by correcting for the density of water.
For some, the difference in accuracy may not be worth it in the field, but it depends on what you are trying to solve. Stay tuned for more details on better sensible heat rate equations.
—Michael








Comments
To leave a comment, you need to log in.
Log In