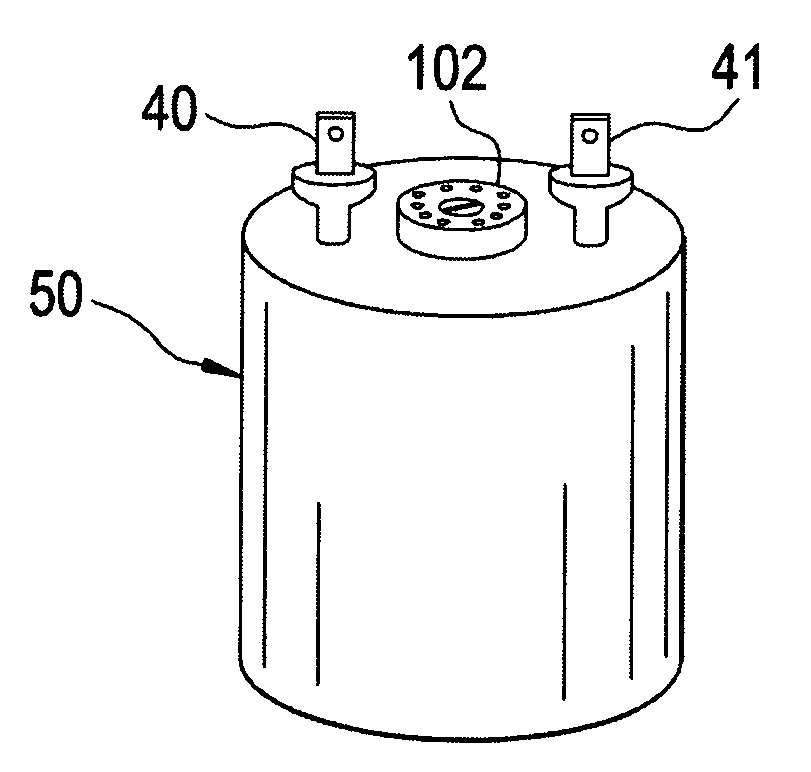
When testing a run capacitor, many techs pull the leads off and use the capacitance setting on their meter to test the capacitor. On a system that is not running, there isn't anything wrong with this test. However, when you are CONSTANTLY checking capacitors as a matter of regular testing and maintenance, that extra step of pulling the connectors off can be time-consuming. In these cases, it is also totally unnecessary. Testing the capacitors UNDER LOAD (while running) is a great way to confirm that the capacitor is doing its job under real load conditions, which is also more accurate than taking the reading with the unit off.

First, if you are used to doing capacitor checks during the “cleaning” stage of a PM, you will need to change your practices and do your tests during the “testing” phase. You will take these readings at the same time you are taking other amperage and voltage readings during the run test.

This method is practical and is a composite of two different test practices combined –

1. Read your Volt (EMF) and Amp (Current) readings like usual and note your readings.

2. Measure the amperage of just the start wire (wiring connecting to the start winding). It will be the wire between your capacitor and the compressor. When it comes to 4-wire motors, it will usually be the brown wire, NOT the brown with a white stripe. Note your amperage on this wire.

3. Measure the voltage between the two capacitor terminals. For the compressor, that would be between HERM and C; for the condenser fan motor, that would be between FAN and C. Note the voltage readings.

4. Now, take the amp reading you took on the start wire (wire from the capacitor) and multiply by 2,652 (some say 2650 but 2652 is slightly more accurate). Then, divide that total by the capacitor volts you measured. The simple formula is Start Winding Amps X 2,652 ÷  Capacitor Voltage = Microfarads.

5. Read the nameplate MFD on the capacitors and compare it to your actual readings. Most capacitors allow for a 6%+/- tolerance. If it's outside of that range, then replacement of the capacitor may be necessary. Always double-check your math before you quote a customer. We need to make sure we are accurate when advising a repair.

6. Repeat this process on all of the run capacitors, and you will have assurance whether they are fully functional under load or not.

7. Keep in mind that the capacitor installed may not be the CORRECT capacitor. The motor or compressor may have been replaced, or someone may have put in the wrong size. When in doubt, refer to the data plate or specs on the specific motor or compressor.

If you need a visual, we've linked some good videos on the topic at the end of this article. Note that some will use 2650, some 2652, and some 2653. It all depends on how many decimals of pi they are using in their calculation, but all of them will result in an accurate enough conclusion for our use.

At first, doing it this way may take a few minutes longer. Still, in the long run, you will go quicker, have fewer mistakes (forgetting to put the terminals back), have a better understanding of how the equipment is operating, and get a more accurate reading.

Once you replace a capacitor, always recheck your readings to ensure the new capacitor reads correctly under load.

It is also a good practice to check capacitors you have removed with your capacitance setting on your meter as a reference point.

While this method is good, it is only as good as your tools and your math. When in doubt, double-check… and always be in doubt.

—Bryan