#ohms

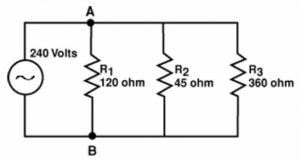
In a series circuit (loads connected in a row end to end), it's easy to calculate total circuit resistance because you simply add up all the resistances to get the total. In a parallel circuit, the voltage is the same across all the loads; the amperage is simply added up, but the resistance is a […]

Some quick basics – An ohmmeter is used to measure the resistance to electrical flow between two points. The ohmmeter is most commonly used to check continuity. Continuity is not a “measurement” as much as it is a yes/no statement. To say there is continuity is to say that there is a good electrical path […]

Ohm’s law is pretty straightforward; you multiply ohms by amps to get the voltage. Using variable E to represent voltage, variable I for amps, and variable R for ohms, the equation for Ohm’s law looks like this:  E = I × R  You can figure out the number of amps in a system using basic […]

  One of the most common mistakes I hear techs make is confusing zero ohms with infinite ohms. The fuse above is showing near-zero ohms, which indicates a good electrical path with very little resistance. If there is a perfect path, it would have zero ohms (which isn't actually possible unless you happen to be […]

 In this episode, Bryan and Bert dive into the often misunderstood world of compressor testing, focusing on common mistakes technicians make when using ohmmeters, compressor testers, and megohm meters. The conversation highlights how diagnostic errors can lead to unnecessarily condemned compressors and wasted time and resources. The hosts begin by discussing fundamental concepts like […]