Another follow-up article by Michael Housh… Enjoy!

In this article, I thought I would show a pump curve and match it up with our system head-loss curve that we created in the last article, but before I do that, I thought I would talk a little bit more about the system head-loss curve and why I said it was so valuable.

When we design a hydronic system, we must match flow rates and output according to our Manual J and the specifications for the radiator/panel being utilized (sort of like Manual S on the air side of HVAC). Here’s an example output specification for a baseboard radiator that I found on the web.

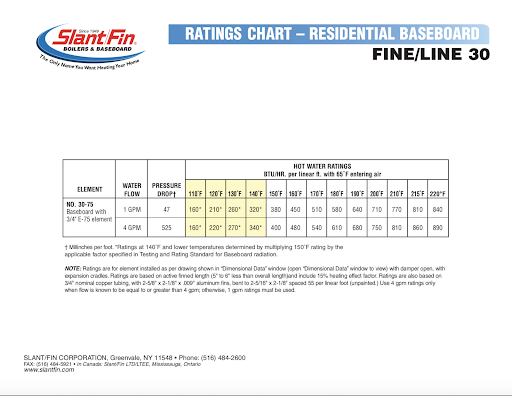
You’ll notice that it gives two different output rows (1 GPM or 4 GPM). You may also notice that the output is relatively close for both flow rates. It is safe to assume that we can move 1 GPM with less power consumed than moving 4 GPM. Let’s check the difference using the head-loss equation from the last article.

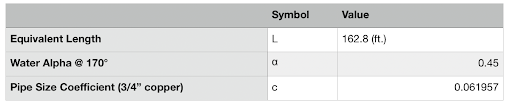
This system is so small that most circulators will produce more than enough flow, but you could maybe imagine how this could greatly affect a much larger or more complicated piping arrangement.

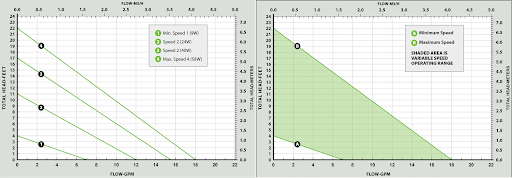
Next, let’s look at a pump curve. The following is for a Taco VT2218; this pump fits a ton of applications, is variable speed, and maintains a constant delta T across our system. In today’s world, it doesn’t make sense in most applications not to utilize an advanced pump, in my opinion. Now, using our 4 GPM and 5.13 ft. of head, we can see that we fall somewhere between speed 1 and 2 (or well within the shaded green area on the right), so this pump will be great for this application (and hopefully sized right for future exercises where make the piping arrangement more complex).

To end the article, I thought I would follow up with more detail on the flow coefficient (Cv) mentioned in the last article for our air-separator. It is not uncommon for items to have a Cv value instead of an equivalent length in design. If you remember from the last article, Cv is the amount of flow (GPM) required at 60° water (important because of density) to create a 1 psi pressure drop across the device. We can use the following equation to convert Cv to pressure drop for our design conditions using the following formula:

Given the above equation, we can solve for our pressure drop using the design criteria of 170° and a flow rate of 4 GPM.  The density of water at 170° is 60.81.

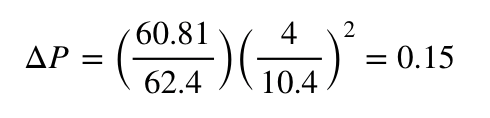
Using the equation from the determining pump flow article, we can convert this pressure drop to feet of head.

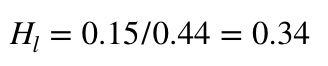
Finally, we can solve for the equivalent length for a given pipe size coefficient using a rearranged version of our system head-loss equation from the previous article.

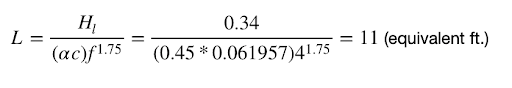
I hope this has helped you gain a deeper understanding of selecting a circulating pump and how to convert a flow coefficient (Cv) into an equivalent length. In future articles, I hope to create a more complex piping arrangement to show the pump selection and equivalent lengths for those applications.

—Michael