Short #8 Resistance Up, Amps Down (Podcast)

This short podcast episode covers the most misunderstood portion of Ohm's law explained masterfully from 1921: when resistance goes up, amps go down.

The American Electrician's Handbook (1921) contains a lot of electrical knowledge that holds up in the present day. (The electrical testing methods don't hold up quite as well, though…) One of those principles that hold up is the idea that amps go down as resistance goes up. Amps refer to current (electrons). The ohm is the unit of electrical resistance, and it is NOT the same as mechanical resistance, such as in a compressor with locked-up bearings.

The common “water” analogy for electricity works quite well for helping us see how voltage enters the equation. Electromotive force (EMF) is comparable to water pressure, which pushes water in a hydraulic piping system. So, you can compare voltage to PSI. The current (amps, I) is comparable to the flow of water. So, if you have more pressure inside a hydraulic system, more water will flow out; as voltage (V) increases, amperage also increases. That analogy also explains why you can have volts without amps; there can be plenty of water pressure behind a closed valve, but there will be no flow.

Additionally, a smaller pipe has more resistance than a large one. So, less water (amps, I) will flow through a pipe with greater resistance (ohms, R). When resistance goes up, amps go down; the water analogy illustrates that principle very clearly in terms that we are familiar with.

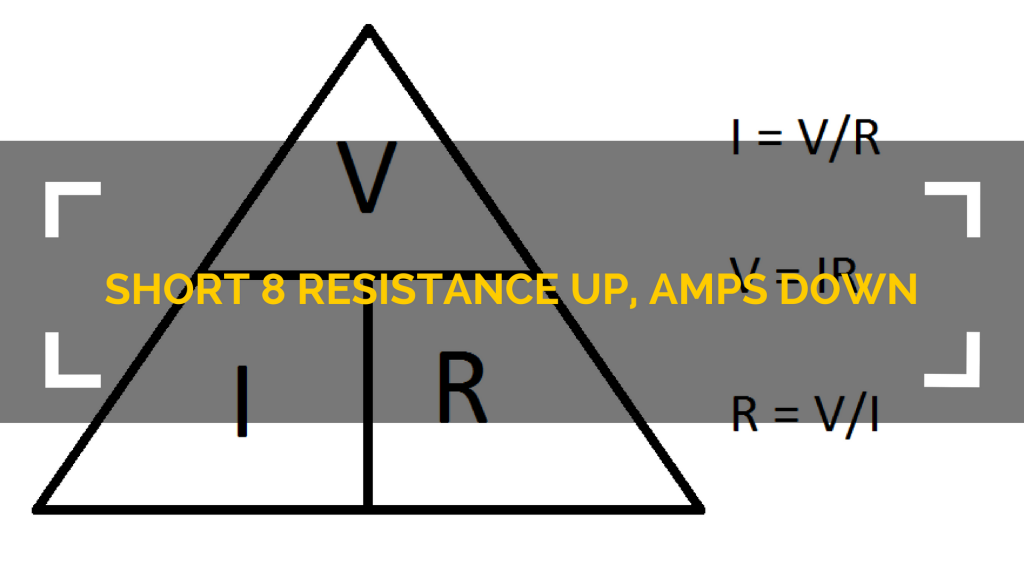
With all these in mind, you can yield the three following equations that make up Ohm's law:

I = V/R

V = I x R

R = V/I

Learn more about Refrigeration Technologies chemical products HERE.

If you have an iPhone, subscribe to the podcast HERE, and if you have an Android phone, subscribe HERE.