“Isaac Newton” by paukrus is licensed under CC BY-SA 2.0

Sir Isaac Newton was an English physicist and mathematician born in a small Lincolnshire village called Woolsthorpe in 1642. His father died before he was born, and his mother remarried when Newton was three years old. He stayed with his maternal grandparents thereafter, and his grandmother taught him how to read and write.

Newton grew up in a tumultuous time for the English government, as the English Civil War began around the same time he was born. By the time Newton reached university age, England had gone through three different monarchs and separated its higher education systems from the Anglican Catholic Church. Charles II rose to power in 1660 and restored religion to the universities. Still, the educational landscape had already changed quite a bit from Newton’s youth to his university years.

In 1661, Newton began attending Trinity College, a constituent college of Cambridge University. He studied philosophy there, primarily focusing on Aristotlean logic, physics, and ethics. He also studied mathematics beyond his curriculum. However, the plague descended upon England during Newton’s university years, forcing Cambridge University to close and Newton to move back home to Woolsthorpe from 1665 to 1667.

Despite the apparent setback, Newton was highly productive during his years away from school. He performed his initial experiments in the new field of optics, a branch of physics that focuses on light’s properties. He also built upon Kepler’s laws to describe the placement and movement of objects in space, gravitational forces on Earth and outer space, and the tides’ relationship with the moon.

By his mid-twenties, Newton had arguably become the best mathematician in the world, as he expanded upon well-known equations and discovered calculus. He returned to Trinity College in a fellowship program, where he further developed his research and discoveries in optics and calculus. In 1669, he became the Lucasian Professor of Mathematics at Trinity, less than five years after receiving his B.A.

Newton continued his mathematical research as a Lucasian Professor, though many of his findings remained unpublished and caused him to lead a life of isolation. He also studied physics in detail, expanding on optics again and diving into planetary orbits, conic trajectories, and forces. In 1687, he published these works in his Principia, a series of three books on his discoveries and mathematical concepts. The publication of Principia jolted Newton into the limelight again after many years of isolation.

Newton published multiple editions of Principia throughout his life. It was the main body of work that contained his discoveries, including his three laws of motion.

Newton’s First Law

Newton’s First Law states that an object at a constant velocity will remain at that velocity unless a net force acts upon it. Velocity refers to speed and direction, so an object may either move in a continuous straight line or have zero velocity, meaning that it is at rest. Another term for this law is inertia, or a general tendency to remain unchanged.

A perfect example of this is that a soccer ball lying in the grass will remain motionless until somebody kicks it. When somebody kicks a soccer ball in a straight line, however, it will eventually slow down. That seems to contradict Newton’s First Law, but the grass provides a source of friction, which is a force that acts against the ball’s motion.

Another example deals with centripetal force, which you can generate when you play with a tetherball. The ball rotates around a central point on a string or rope. However, if the rope breaks, the ball will not continue to spin because the centripetal force no longer acts on it. Instead, it will fly off in a straight line, tangentially from where the string broke. You can see this in action below.

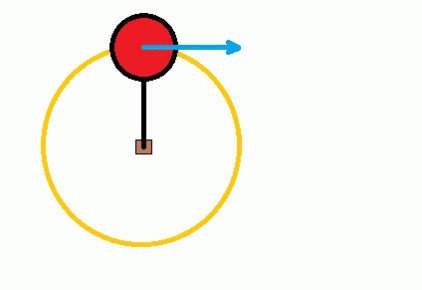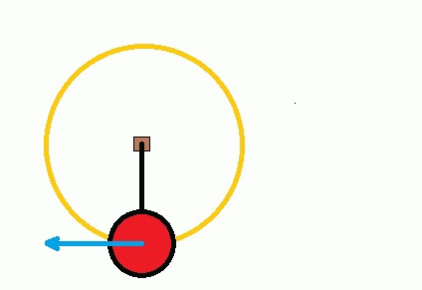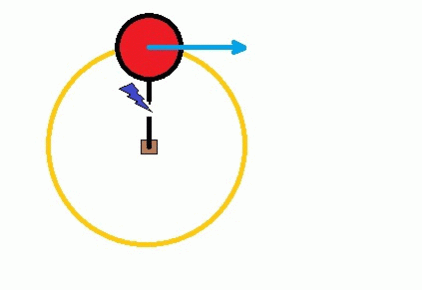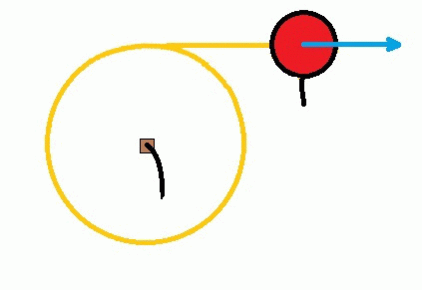
AlvaroLopez12, CC BY-SA 4.0 via Wikimedia Commons

Newton’s Second Law

Newton’s Second Law addresses the net force that must act on an object. It states that net force equals an object’s mass multiplied by its acceleration. (You may recognize the equation F = ma.) 

We measure force in units called newtons (N), mass in kilograms (kg), and acceleration in meters per second squared (m/s²). As such, you could rewrite F = ma like this:

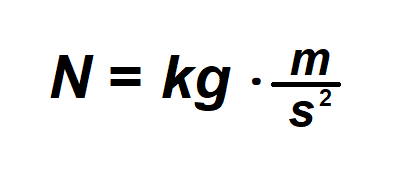
Since a newton is equivalent to mass times acceleration, you can represent N values as kilograms times meters per second squared.

Let’s say that someone slides a 10-kilogram box on the floor with 50 newtons of force.  You can find the acceleration by plugging in the N and kg values as such:

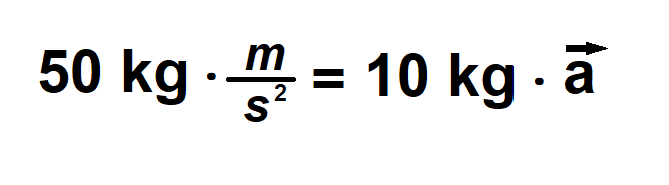
The arrow above the a indicates the direction of the motion. Acceleration and force are vectors, meaning that they indicate direction. To solve for the missing acceleration, divide each side by the mass (10 kg) to eliminate the kilograms and leave only the acceleration unit (m/s²).

Newton’s Third Law

Newton’s Third Law states that every force has an equal and opposite force. This law may seem a bit counterintuitive, as you can push a piece of furniture and move it forward. If it were pushing back with an equal and opposite force, wouldn’t it stay in the same place? Wouldn’t every force cancel out, leaving us with no acceleration?

It might seem that way, but that’s NOT the case. Although pairs of objects exert forces on each other, the opposite force is exerted on a different object. For example, when you push a chair, you exert force on the chair. The chair doesn’t exert the opposing force on itself; it exerts the force on your hand (or the body parts that push the chair). That’s why you feel a bit of resistance whenever you push a piece of furniture.

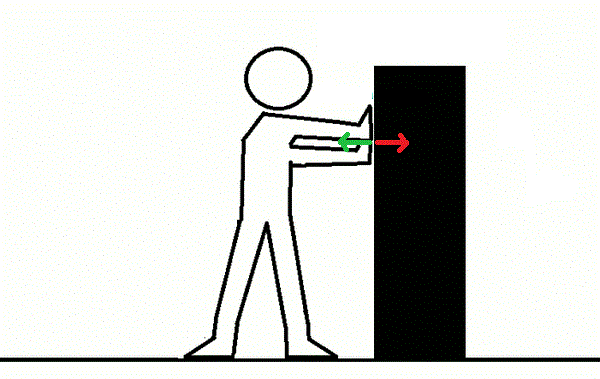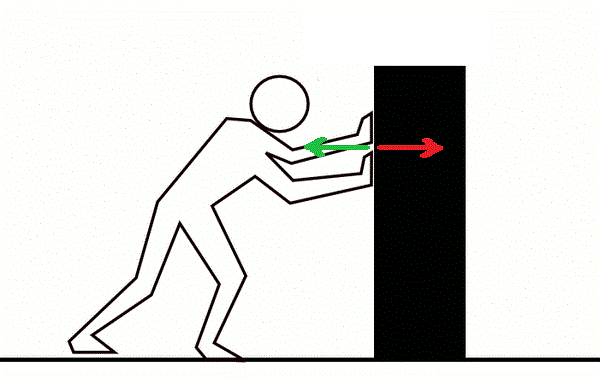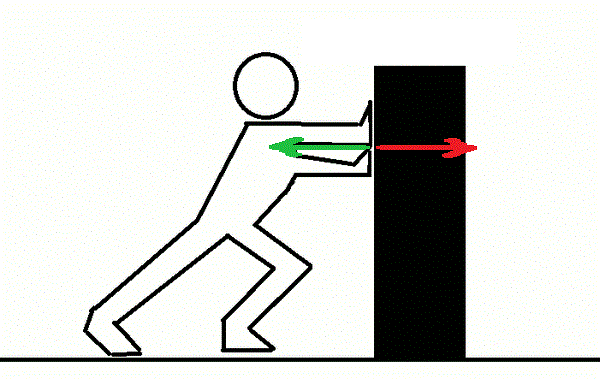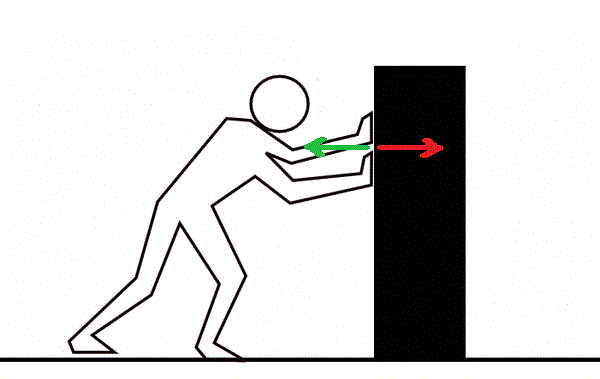
AlvaroLopez12, CC BY-SA 4.0 via Wikimedia Commons

It’s also worth noting that the forces will be equal, but the resulting accelerations may not be. That’s why you can slide a chair four feet on the floor without the chair sending you backward four feet. (Your palms may have imprints from the chair, and your muscles may feel slightly fatigued, but you certainly won’t slide back the same distance you pushed the chair.) The accelerations are nowhere near the same, even if the forces are. 

The Third Law is also why your foot hurts A LOT when you kick a heavy machine out of frustration. The device may not move because of its large mass, but it exerts a painful amount of oppositional force on your foot!

We may not see Newton’s laws directly measured in HVAC, at least not to the same extent as gas laws or laws of thermodynamics. However, Newton’s laws help us understand that nothing can start until something provides the force to make it start. Each exertion of force depends on the mass and acceleration of the exertion, and each application of force has consequences on both objects involved. These laws lay the groundwork for all the motion we see in our everyday work and beyond the HVAC/R field.

References

http://hyperphysics.phy-astr.gsu.edu/hbase/Newt.html 

https://www.khanacademy.org/science/high-school-physics/forces-and-newtons-laws-of-motion/newtons-second-law/v/newton-s-second-law-of-motion 

https://www.khanacademy.org/science/high-school-physics/forces-and-newtons-laws-of-motion/newtons-third-law-2/v/more-on-newtons-third-law 

https://plato.stanford.edu/entries/newton/ 

Special thanks

Modern Refrigeration and Air Conditioning, 21st edition (Andrew Althouse, Carl Turnquist, Alfred Bracciano, Daniel Bracciano, and Gloria Bracciano)

Refrigeration & Air Conditioning Technology, 9th edition (Eugene Silberstein, Jason Obrzut, John Tomczyk, Bill Whitman, and Bill Johnson)

These truly are the reference guides for the industry and deserve attribution for all such articles.