In HVAC and electrical school, one of the first things you learn about electricity is Ohm's law:

Volts (V) = Amps (I) x Ohms (R)

Pretty simple, right? Watt's law is just as easy:

Watts (P) = Volts (E) x Amps (I)

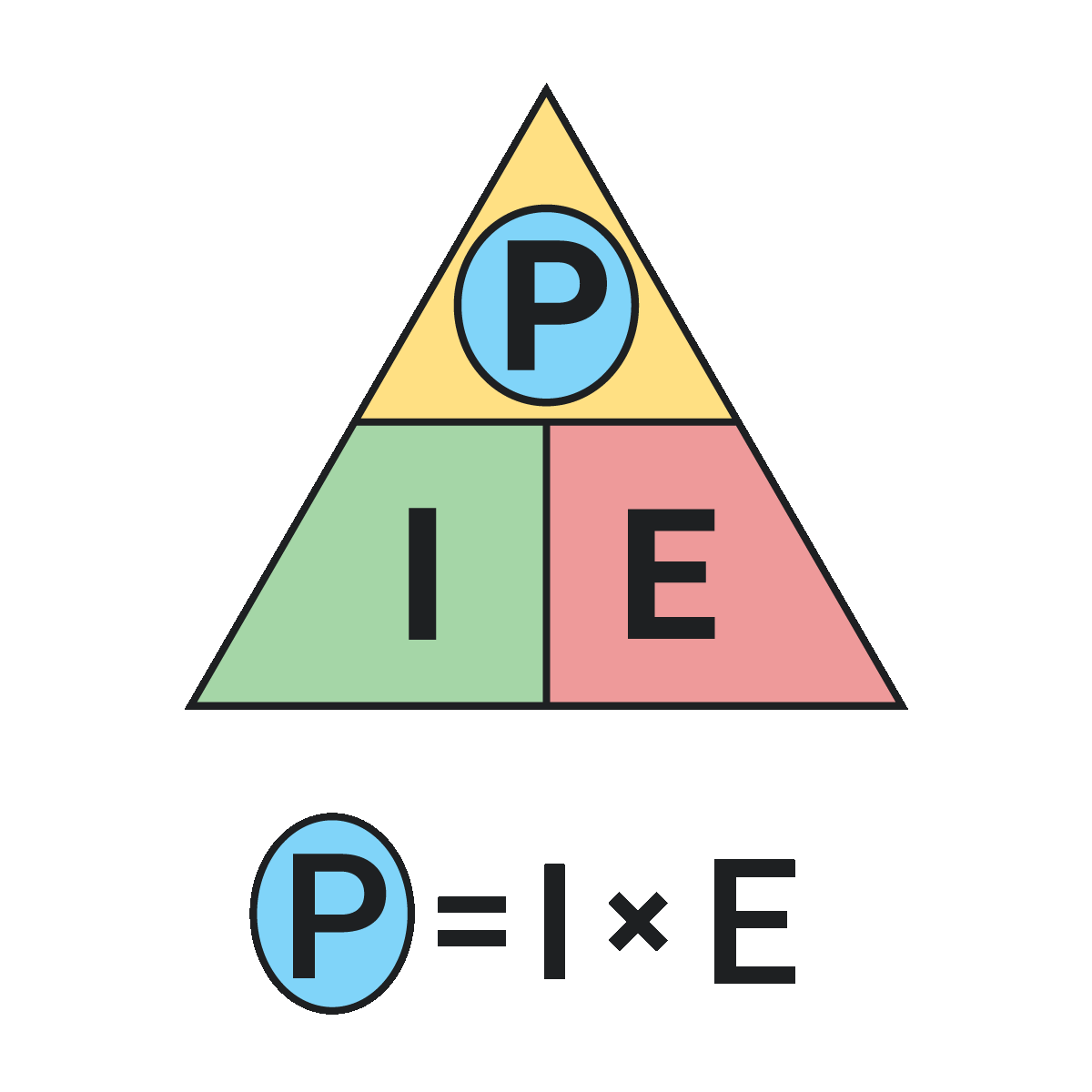
With this newfound knowledge, the student walks confidently into the real world with two equations and some elementary algebra skills, expecting to be able to predict volts, amps, watts, and ohms using this secret knowledge.

Then they ohm out a residential compressor or other single-phase motor windings for the first time…

They might read something like:

Start to Common = 4.2 ohms

Run to Common = 2.6 ohms

Start to Run = 6.9 ohms

So, they measure their voltage, grab a calculator, and calculate.

Run Winding 243V ÷ 2.6Ω = 93.4A

Start Winding 243V ÷ 4.2Ω = 57.85A

Well, THAT makes no sense, so they stop using Ohm's law and settle for believing that electricity is magic and Ohm's law is broken.

In actuality, Ohm's law does work; it's just that the loads we measure tend to vary and don't all behave in the same way.

Inductive Loads

In the case above, a compressor/fan motor/contactor coil, etc., is an inductive load. That means that its job is to convert electrical energy to an electromagnetic force. While an inductive load does have SOME resistance when de-energized that can be measured with an ohmmeter, the majority of the electrical resistance only shows up once the current is applied.

In an inductive (magnetic) load, this resistance that shows up once it's powered on is called inductive reactance and is still measured in ohms. If you want to learn more about inductive reactance, please check out this article HERE.

In the case of the example we've been following, the run winding is connected directly between L1 & L2. When the contactor completes the circuit, the run winding WILL actually draw really high amps for a split second (first electrical cycle) until the inductive reactance kicks in.

In the start winding, the current is limited by a combination of resistance, inductive reactance, and the capacitance of the capacitor. Add in the fact that the applied voltage across the run winding is actually higher than the L1-L2 voltage due to back EMF (CEMF), and it's enough to confuse anyone.

Then you throw power factor into the mix in an inductive load, which means that even when we multiply volts x amps in an inductive AC circuit, what we see in VA isn't necessarily what you get in watts.

It takes a lot of measurements and math to figure this all out. Unless you are an engineer, it's much easier to measure what you have on a functioning component rather than attempting to calculate amperage and wattage based on voltage and ohms.

However…

We are taught that resistive loads (loads that create light and heat) are much simpler. There is none of this inductive reactance or power factor nonsense in a resistive load like a light bulb or a heat strip.

But wait, there's more!

So, this light bulb is measuring 12.2 ohms, confirmed with two different meters, and rated at 14.4 volts. So, we do the simple math:

Amps = 14.4v ÷ 12.2Ω 

Therefore, amps = 1.18

So, we put it to the test by feeding this bulb exactly 14.4V from a DC power supply:

Annnnddd… it's not even close.

We expected an amperage of 1.18 and got an amperage of 0.1.

SO, WHAT THE HECK IS GOING ON?

Incandescent light bulbs are a resistive load, but they are also made with a filament of the element tungsten, which has PTCR (positive temperature coefficient resistor) properties. That means that the resistance of a tungsten incandescent light bulb increases 10 to 15 times its cold temperature to its hot temperature. In the case of the bulb above, we know its cold resistance is 12.2 ohms, but by working Ohm's law backward, we can also tell that its HOT resistance is 142.57 ohms, which means that the hot resistance is 11.6 times higher than cold in this particular instance.

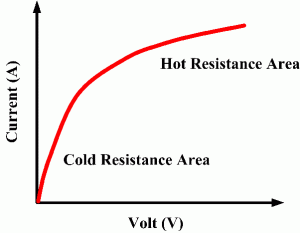
Not all resistive loads behave in this way, though. Let's look at a heat strip.

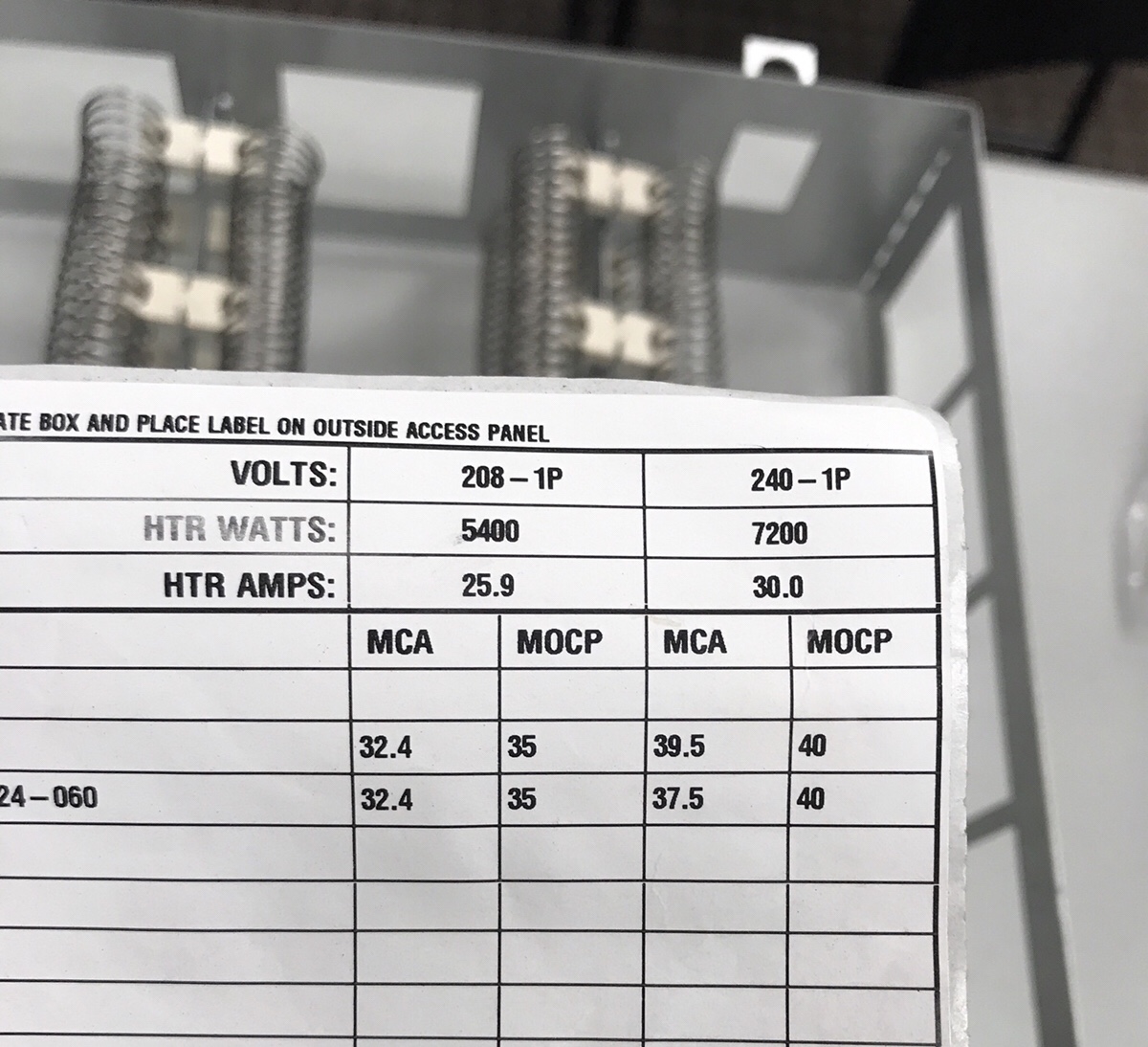
Amps = 240v ÷ 15.5Ω

Amps = 15.48 

Watts = 240v x 15.48

Watts = 3715 based on Ohm's & Watt's laws

Don't worry. We're using a 7.2kw (7200-watt) heat strip divided into two 3600-watt strips, and we are only reading one half (3.6kw).

To bench test it further, I applied one-tenth of the designed voltage (24 volts) to see how it would respond.

1.532a @ 24v = 15.32a @ 240v 

The math still doesn't line up perfectly because even in a heat strip, the resistance increases as the temperature increases, but it's in a much smaller fashion than in a light bulb.

When cold, the math predicts it is a 3.7kw heater; when warm at 24v applied, it predicts 3.67kw, and at 240v, the resistance increases to its full rating at 3.6kw.

All of this to say that Ohm's & Watt's laws are useful and accurate, but they are impacted by real “under load” forces in such a way that it is much more realistic to make measurements on a functioning device and work backward than to use ohms to work upwards from an ohm bench test and a voltage.

—Bryan